Staircase
Calculus
Much of the intuition behind the calculus you see in school actually comes from understanding how staircases work. Compared to school calculus, the mathematics of staircases—more commonly known as finite calculusOther names for finite calculus: discrete calculus, sequence calculus, calculus of finite differences. —is much simpler. In fact, here is what the Fundamental Theorem of Finite Calculus tells us.
Surprisingly, this Fundamental Theorem can help us compute complicated sums. To do this, we first need our staircases to follow some pattern.
The simplest pattern is the Natural Numbers Staircase, where the first rectangle has height 1, the second rectangle has height 2, and so on. Everything we discuss here also works if we replace the natural numbers by the integers, resulting in the Integer Staircase that extends both leftward and rightward:
The Square Numbers Staircase is built from rectangles whose heights are square numbers: the first rectangle has height $1^2=1\times1=1$, the second has height $2^2=2\times2=4$, the third has height $3^2=3\times3=9$, and so on.
Finally, the General Staircase is built from rectangles of height $f(n)$ where $f$ is a function with natural numbers inputs $n$.
As special cases of the General Staircase, we get back the Natural Numbers Staircase when $f(n)=n$ and the Square Numbers Staircase when $f(n)=n^2$.
Subtract rectangle heights to get step heights
Clearly the step heights in the Natural Numbers Staircase are all $1$. The Square Numbers Staircase is more interesting—as you walk right, its step heights are increasing odd numbers.
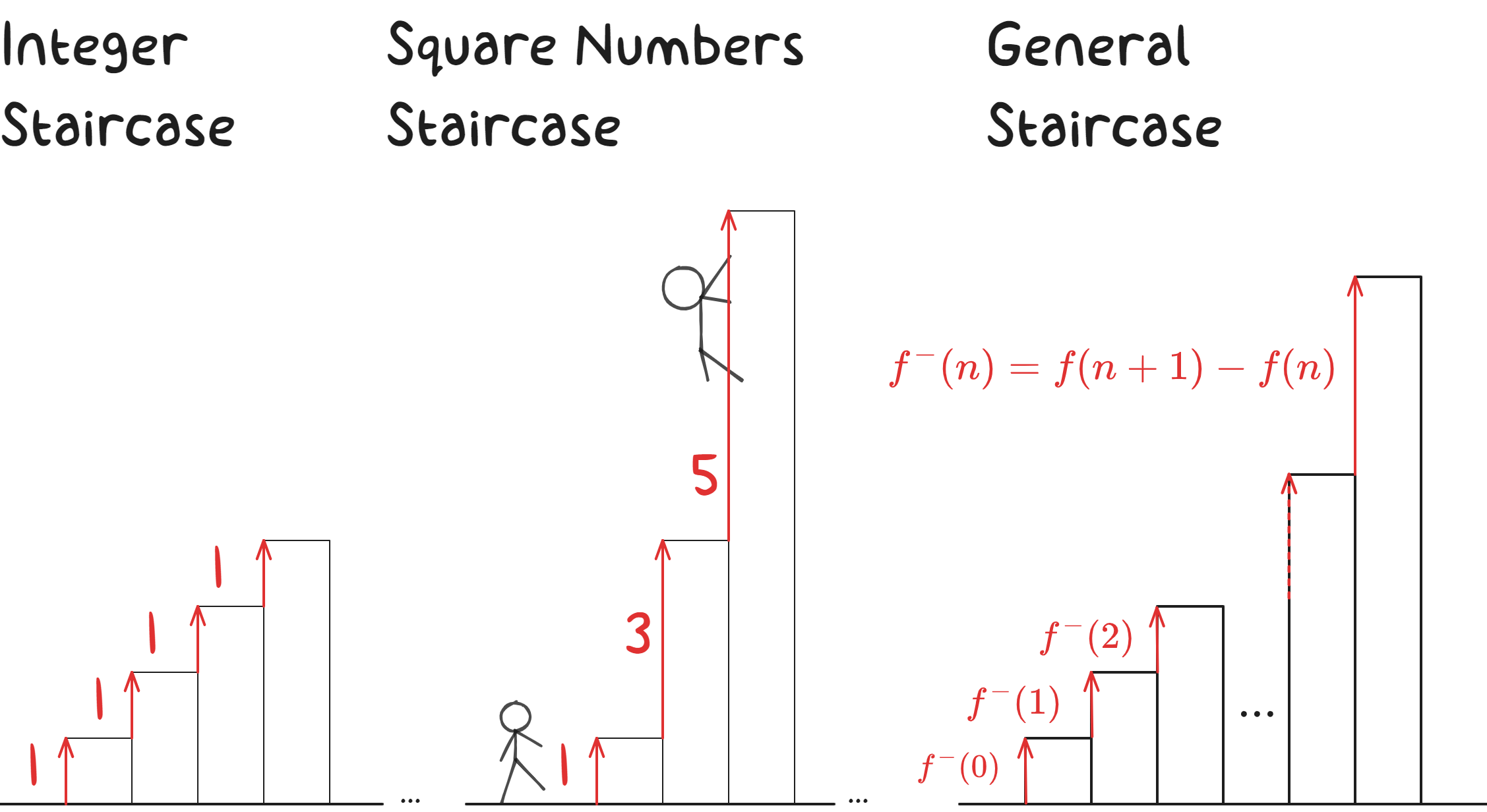
In general, the $n$th step height is the difference in height between the $n$th rectangle and the $(n+1)$st rectangle. So in the General Staircase, the $n$th step height is $$f^{\htmlId{hMinus1}{-}}(n)=f(n+1)-f(n).$$ We introduce this handy superscript minus sign notation to remind us to subtract. Therefore the $n$th step height of the Natural Numbers Staircase and the Square Numbers Staircase can also be calculated algebraically as follows.
| $\boldsymbol n$th step height | |
|---|---|
| General Staircase | $$f^-(n)$$ $$=f(n+1)-f(n)$$ |
| Natural Numbers Staircase $\small f(n)=n$ | $$(n)^-$$ $$=(n+1)-n$$ $$=1$$ |
| Square Numbers Staircase $\small f(n)=n^2$ | $$(n^2)^-$$ $$=(n+1)^2-n^2$$ $$=2n+1$$ $$=\text{odd number}$$ |
Add step heights to get elevation gain
Recall that the Fundamental Theorem of Finite Calculus says that the step heights you have taken add up to your elevation gain.
With the Natural Numbers Staircase, this means that the difference of two numbers is a sum of that many $1$'s.
With the Square Numbers Staircase, this means that the difference of two square numbers is a sum of consecutive odd numbers.
Now consider the General Staircase whose $n$th rectangle height is $f(n)$. If we walk from its $a$th rectangle up to its $b$th rectangle, the resulting picture looks like this:
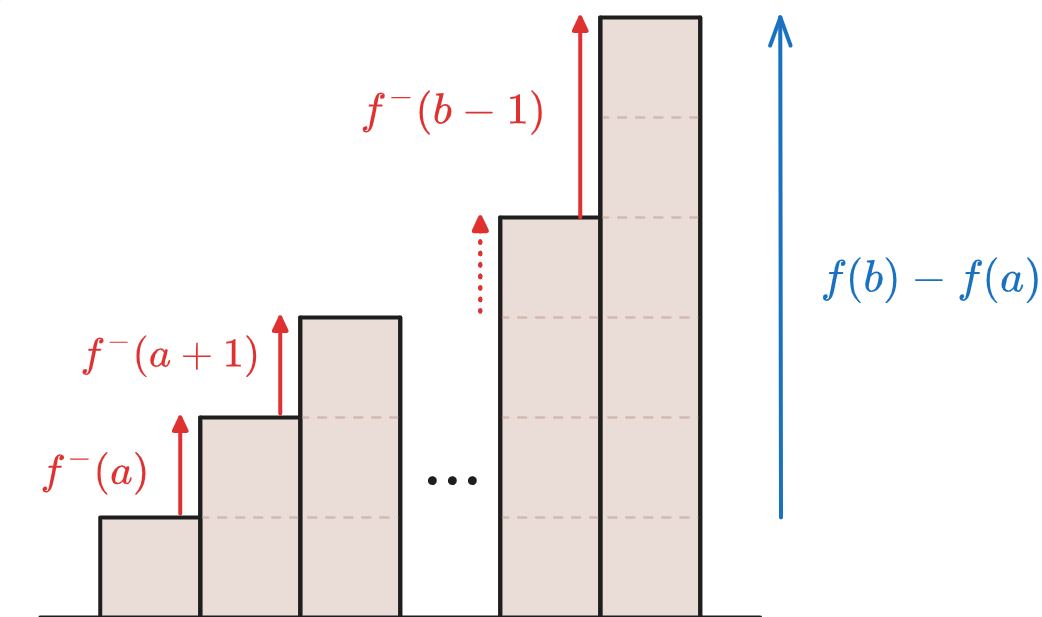
Thus the Fundamental Theorem is written algebraically as
or more elegantly as $$\htmlId{hLeftSum2}{\sum_{n=a}^{b-1}f^-(n)} = \htmlId{hRightDifference2}{f(n){\Large\vert}^b_a}$$ upon adopting new notations $\Sigma$ and $\vert$. Here we read
- $\displaystyle\sum_{n=a}^{b-1}f^-(n)$ as
$f^-(n)$ summed from $a$ to $b-1$
, and - $f(n){\Large\vert}^b_a$ as
$f(n)$ evaluated from $a$ to $b$
.
The evaluation bar notation $f(n){\large\vert}^b_a=f(b)-f(a)$ simply performs subtraction. The summation notation $\Sigma$ is way more awesome since it shortens a sum like $$1^2+2^2+3^2+4^2+\cdots+98^2+99^2+100^2$$ $$\begin{split}1^2+2^2&+3^2+4^2+\cdots\\&+98^2+99^2+100^2\end{split}$$ to just $\displaystyle\sum_{n=1}^{100}n^2.$
Here is what the Fundamental Theorem looks like for the Natural Numbers Staircase, the Square Numbers Staircase, and what we will call the Exponential Staircase
.
| Step heights | Fundamental Theorem | |
|---|---|---|
| General Staircase | $$f^-(n)$$ $$=f(n+1)-f(n)$$ | $$\sum_{n=a}^{b-1}f^-(n)$$ $$=f(n){\Large\vert}^b_a$$ $$=f(b)-f(a)$$ |
| Natural Numbers Staircase $\small f(n)=n$ | $$(n)^-=1$$ | $$\sum_{n=a}^{b-1}1$$ $$=n{\Large\vert}^b_a$$ $$=b-a$$ |
| Square Numbers Staircase $\small f(n)=n^2$ | $$(n^2)^-$$ $$=2n+1$$ | $$\sum_{n=a}^{b-1}(2n+1)$$ $$=n^2{\Large\vert}^b_a$$ $$=b^2-a^2$$ |
| Exponential Staircase $\small f(n)=r^n$ | $$(r^n)^-$$ $$=r^{n+1}-r^n$$ $$=(r-1)r^n$$ | $$\sum_{n=a}^{b-1}(r-1)r^n$$ $$=r^n{\Large\vert}^b_a$$ $$=r^b-r^a$$ |
| Step heights / Fundamental Theorem | |
|---|---|
| General Staircase | $$f^-(n)$$ $$=f(n+1)$$ $$-f(n)$$ |
$$\sum_{n=a}^{b-1}f^-(n)$$ $$=f(n){\Large\vert}^b_a$$ $$=f(b)-f(a)$$ | |
| Natural Numbers Staircase $\small f(n)=n$ | $$(n)^-=1$$ |
$$\sum_{n=a}^{b-1}1$$ $$=n{\Large\vert}^b_a$$ $$=b-a$$ | |
| Square Numbers Staircase $\small f(n)=n^2$ | $$(n^2)^-=2n+1$$ |
$$\sum_{n=a}^{b-1}(2n+1)$$ $$=n^2{\Large\vert}^b_a$$ $$=b^2-a^2$$ | |
| Exponential Staircase $\small f(n)=r^n$ | $$(r^n)^-$$ $$=r^{n+1}-r^n$$ $$=(r-1)r^n$$ |
$$\sum_{n=a}^{b-1}(r-1)r^n$$ $$=r^n{\Large\vert}^b_a$$ $$=r^b-r^a$$ |
In these examples, notice that subtraction formulas reverse into summation formulas. Ignoring subscripts and superscripts:
- $(n)^-=1$ reverses into $\sum 1=n$, and
- $(n^2)^-=2n+1$ reverses into $\sum (2n+1)=n^2$.
In other words, the Fundamental Theorem gives us a strategy to compute a sum $\sum g(n)$:
- First recognize $g(n)$ as the differences $f^-(n)$ of some $f(n)$.
- Next apply the Fundamental Theorem to conclude$$\sum_{n=a}^{b-1}g(n)=f(b)-f(a).$$
Finite calculus
There is actually a bit more to finite calculus.
We already saw how subtraction gets interpreted geometrically—take two adjacent rectangles and subtract their heights to get the step height.
With addition though, the preferred geometric interpretation in finite calculus is in terms of signed areas. Here is how this works.
Add rectangle heights to get signed area
Start with flat land.
If we build a square mound, we gain one square of dirt.
If we dig a square hole, we lose one square of dirt.
Overall, the signed area of a shape is how much dirt we gain or lose compared to the barren, flat land we started with—it is the sum of the positive heights (for mounds) and the negative heights (for holes).
We use the term signed area because mounds are assigned positive areas, while holes are assigned negative areas.
The next picture shows a signed area of zero due to cancellations between positive and negative areas. So this landscape has the same amount of dirt as the original flat land.
Visualizing sums as signed areas is pretty nifty because simple shapes have simple areas. For instance, in the same way that we find the area of a triangle, we can also compute the sum
Basic rules
Some basic rules about summation formulas fall out naturally from our new geometric interpretation.
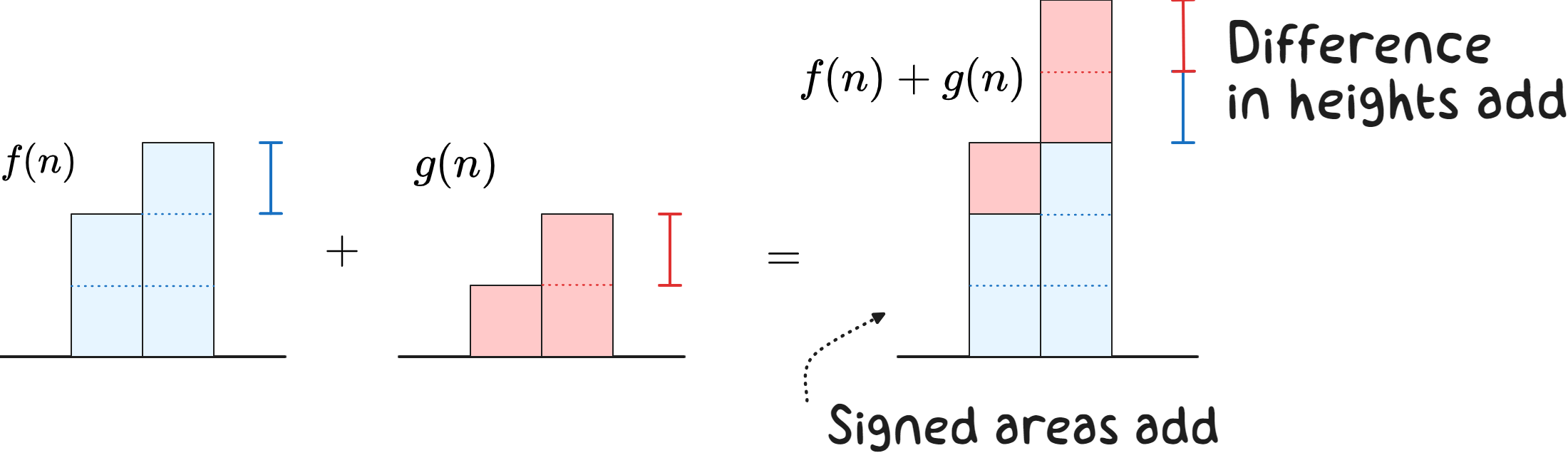
When we add two functions $f$ and $g$, the graph of $f+g$ is just the graphs of $f$ and $g$ stacked together. When we draw this out, the signed areas of these graphs clearly add together. The same is true for their height differences.
Likewise, multiplying a function $f(n)$ by a constant $c$ stretches its graph vertically by $c$. Again, the signed area and height differences also scale by the same factor $c$.
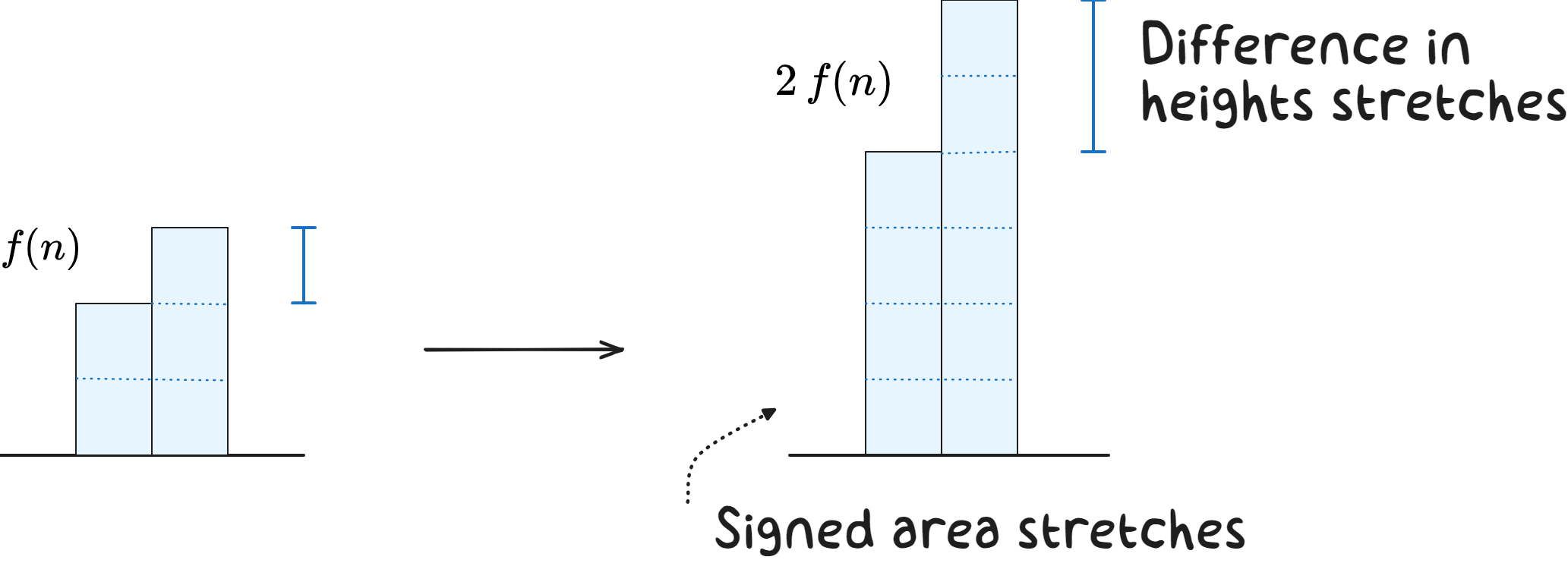
In symbols, the subtraction rules are then $$ \begin{align*} (f+g)^-(n)&=f^-(n)+g^-(n)\\[2ex] (c\cdot f)^-(n)&=c\cdot f^-(n) \end{align*} $$ and the summation rules are $$\sum_{n=a}^{b}\left[f(n)+g(n)\right]=\sum_{n=a}^{b}f(n)+\sum_{n=a}^{b}g(n)$$ $$ \begin{split} \sum_{n=a}^{b}[f&(n)+g(n)]\\ &=\sum_{n=a}^{b}f(n)+\sum_{n=a}^{b}g(n) \end{split} $$ $$\sum_{n=a}^{b}c\cdot f(n) = c\, \sum_{n=a}^{b}f(n)$$
We can find fancier sums by developing finite calculus further, but we'll stop here. Let's now see how school calculus, aka infinitesimal calculus, works.